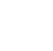5 Chemical Isolation Layer Modeling

Models are useful tools to support remedial design decision-making. Models can be used during any point of the remedial process, including development or refinement of the CSM, feasibility study, design, construction, and post-construction monitoring and maintenance. Models can be used to predict contaminant mass flux and concentrations at various locations and depths within the sediment and cap and to identify cap configurations (i.e., thickness and/or material selection, including amendments) that are suitable for addressing RAOs, including the following: 

• assessment of surface water and surficial sediment quality 
• containment of contaminated sediments 
• minimization of chemical release from the underlying sediments or a cap/CIL 

This section provides an overview of how models are typically used to support cap designs, describes the important processes that affect contaminant transport in sediments, summarizes existing cap modeling software, and discusses how to use these models. 

5.1 Introduction to Modeling Approaches and Tools 

Sediment represents a critical linkage between overlying surface water and underlying groundwater in aquatic systems. Modeling tools are widely used to describe the fate and transport of contaminants in sediment, groundwater, porewater, and surface water. Models are particularly useful for determining cap thickness and the type and quantity of amendment necessary to achieve chemical isolation performance objectives. It is important to understand the potential advantages and limitations of different modeling software to determine the best modeling tools for a given site. Most existing computer models used to analyze contaminants in water systems only simulate a portion of the environment, leaving out other key components such as boundary conditions. For example, surface water quality models require assumptions about the flux of contaminants and other constituents to and from the adjoining atmosphere and sediment column, as shown in Figure 5-1. Therefore, a surface water quality model is well suited for providing an understanding of how sediment contaminants may lead to environmental risks in rivers and lakes, but alone it cannot predict the behavior of contaminants within the sediment column. Likewise, groundwater models can provide important information for sediment management such as seepage rates but typically operate across much larger spatial scales than sediment models and do not simulate key sediment processes such as bioturbation, erosion, and deposition. 

Figure 5-1. Surface water quality modeling domain.

Source: David Lampert. Used with permission.

Computer simulation tools have been developed specifically for analyzing the fate and transport of contaminants in sediments and caps. Two of the most widely used models for the design and evaluation of caps that are discussed in this guidance document are RECOVERY (Boyer et al. 1994; C. E. Ruiz, Schroeder, and Aziz 2000), and CapSim (Shen et al. 2018). Both RECOVERY and CapSim simulate the behavior of contaminants within the sediment column, which may include only sediment (to evaluate natural recovery), cap, or in situ treatment, but neither model attempts to simulate the underlying groundwater. Both CapSim and RECOVERY can simulate a completely mixed or vertically mixed water column above the sediment column. These cap models specifically simulate the near-surface sediments using the overlying water and underlying groundwater as boundary conditions as shown in Figure 5-2. Those boundary conditions may be dynamic and allow estimation of surface water quality, but the sediment and cap models do not explicitly simulate the variety of processes that might occur in the overlying water column. 

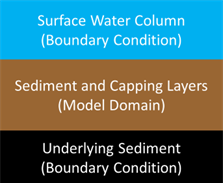
Figure 5-2. Sediment and cap model domain.

Source: D. Lambert. Used with permission. 

At many sites, a capping model may be complemented by additional models that specifically simulate other key aspects of the system. A brief description of these models is provided below. 

5.1.1 Surface Water Quality Models 

Surface water quality models such as CE-QUAL-W2 (Cole and Wells 2006), AQUATOX (Park, Clough, and Wellman 2008), and Water Quality Analysis and Simulation Program (WASP) (Ambrose, Wool, and Martin 1993) can provide important information on the fate and transport of contaminants that are released from sediments; however, they do not explicitly simulate the contaminant release rates from the sediment. CE-QUAL-W2 is a two-dimensional surface water quality model that emphasizes eutrophication processes including temperature, nutrient and algal dynamics, dissolved oxygen, and sediment relationships. CE-QUAL-W2 may be an important complementary tool for sediments where nutrient and organic matter impairments are important. AQUATOX is a surface water quality model that predicts the fate of contaminants including nutrients and organic chemicals and their ecological effects on invertebrates, fish, and aquatic plants. AQUATOX can be an important complementary tool for sediment remediation projects where ecological effects assessment is important. WASP is a dynamic modeling program for aquatic systems that simulates the water column and the underlying benthic community. WASP incorporates advection, dispersion, point and diffuse mass loadings, and boundary exchange to simulate contaminant fate and transport in surface water. WASP can be linked with hydrodynamic and sediment transport models to analyze sediment fluxes, and it represents an important complementary tool for contaminated sediments. In aquatic systems where sediments and caps affect surface water quality, or surface water systems provide important interactions with contaminated sediments, WASP can help improve the representation of the surface water column. 

5.1.2 Hydrodynamic Models 

Water quality models can provide representations of ecological, chemical, and other environmental processes, but their representation of fluid flow is relatively simplistic, often assuming plug flow conditions. Hydrodynamic models can be used to overcome these limitations and develop detailed representations of the fluid flow in surface water bodies. Fluid flow conditions are important for understanding scour and sediment deposition in contaminated areas. The Environmental Fluid Dynamics Code (EFDC) is one of the most widely used hydrodynamic models for surface water bodies (Hamrick 1992). The EFDC is a hydrodynamic model that simulates aquatic systems in one, two, and three dimensions. It includes hydrodynamic, sediment-contaminant, and eutrophication components in a multifunctional system for surface water modeling. Transition zone and surface water contaminant processes are represented through an enhanced version of the EFDC model, AQFATE (Connolly et al. 2000). AQFATE also includes SEDZLJ, a state-of-the-science surface water sediment transport model (Jones and Lick 2001). Delft3D is an open-source, three-dimensional modeling suite that can be used to investigate hydrodynamics and sediment transport in surface water systems (Roelvink and Van Banning 1995). Both EFDC and Delft3D can be used to analyze erosion and deposition of sediments in contaminated areas, which is important complementary information for cap designs. Hydrodynamic models are needed to define cap and sediment stability in contaminated site assessments due to their detailed characterization of the physical characteristics of sediments, but these tools typically have limited representations of chemical behavior in sediments that are needed for cap design. 

5.1.3 Groundwater Models 

Groundwater and surface water are often hydraulically connected with groundwater flowing to surface water or surface water flowing to groundwater depending on the time and setting (Winter et al. 1998). Understanding the groundwater flow conditions is an important component of the CSM (ITRC 2014), and groundwater models are commonly used by hydrogeologists to understand the regional and localized groundwater flow conditions and make predictions about future conditions. 

Many different modeling codes and software are available and capable of simulating groundwater flow. The most common groundwater flow model is the USGS’s finite-difference code MODFLOW, which is considered the international standard groundwater flow modeling code due to its robust, modular simulation capabilities, ongoing development, and decades-long verification and testing (Christian D. Langevin et al. 2017; Christian D Langevin et al. 2022). In addition to finite-difference models, models using finite element formulations, such as FEFLOW (Diersch 2013), and analytic element numerical formulations, such as AnAqSim (Fitts Geosolutions 2022), are also commonly used. In addition, MT3D is often used to model contaminant transport in a cap, but MT3D does not have the sediment-specific processes incorporated, including bioturbation, deposition, erosion, etc. 

Modeling codes and software are also available to simulate complex processes like the fate and transport of contaminants, variably saturated flow, variable density flow, and fully integrated groundwater–surface water flow. The complexity of the hydrologic/hydrogeologic setting and the desired model certainty for a given project should be carefully evaluated prior to selection of a specific modeling tool (Anderson and Woessner 1992). As the complexity of the processes being simulated increases, the data needs, effort, and computational demands increase. 

5.2 Sediment Processes 

Modeling tools that explicitly describe contaminant fate and transport processes within sediments are needed because of the complexity of those processes. These processes are shown in Figure 5-3. 

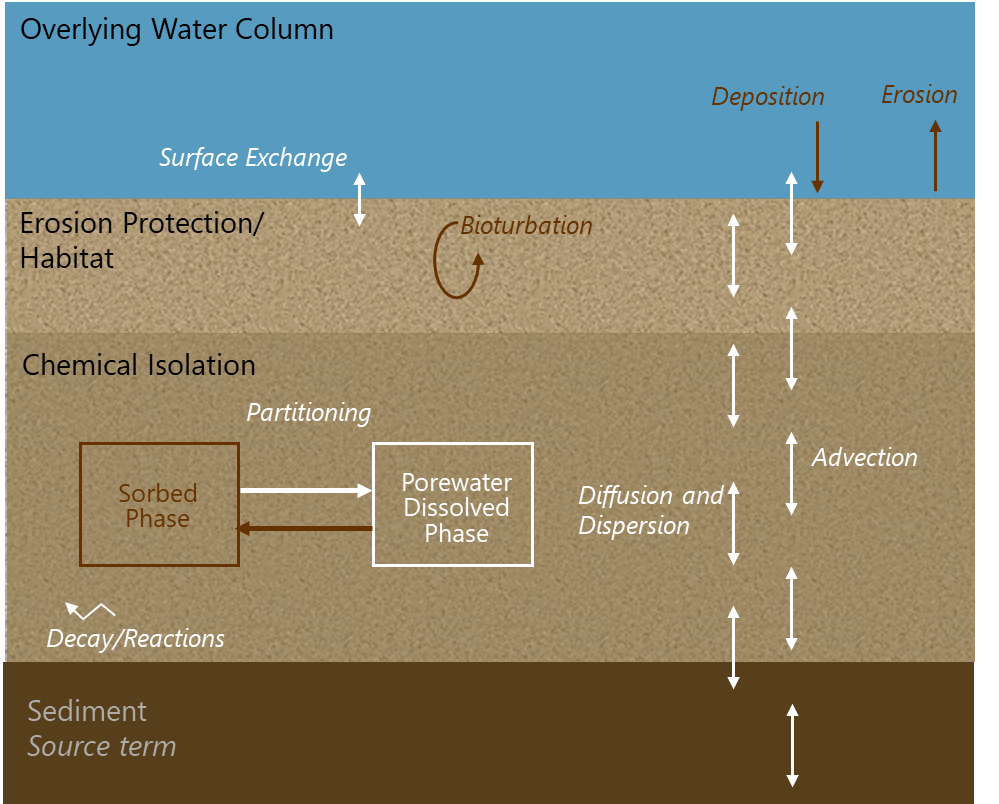
Figure 5-3. Schematic of transport processes. 

Source: Modified from Anchor QEA (2019). Used with permission. 

Because sediment fate and transport models describe the near sediment surface (and rarely extend more than a meter below the sediment–water interface), the primary concern is for one-dimensional transport up or down in the sediment environment. Physical transport processes such as erosion and deposition can be assessed through hydrodynamic models in the overlying water and via measurement of historical deposition (or erosion) rates. Assessment of erosion is normally performed to define the armoring required to ensure that the cap is stable. Deposition might be assessed to evaluate long-term chemical isolation performance, as discussed in Section 3. 

In a stable sediment environment, one not subject to significant erosion, contaminant transport is driven by diffusion and advection processes in the pore space as well as biological processes in the near-surface environment. Hyporheic exchange is an advective process that occurs very close to the sediment–water interface where the overlying water moves into and through the underlying sediment due to either variations in bottom topography or features in the underlying sediment such as burrows or roughness. Advection in the form of groundwater movement (both up in a gaining stream and down in a losing stream) will tend to dominate contaminant migration over all but the top few centimeters of sediment or cap. Groundwater upwelling is of particular concern in that it encourages contaminant movement from underlying sediments into the overlying water. 

Further complicating the near-surface sediment environment is the presence of benthic organisms that burrow into sediments and process the sediment for food. The resulting bioturbation moves contaminants associated with both water and the solid phase and is typically the most important mechanism for transport of hydrophobic contaminants in the near-surface sediment environment. The BAZ is typically 5 to 10 cm in depth but can extend deeper, particularly in marine environments (D.D. Reible and Lampert 2014; USEPA 2005, 2015b; Boudreau 1998; Teal et al. 2008; Clarke et al. 2001). These are normally modeled at the population level (i.e., the cumulative effect of the behavior of the organism, not the individual) using effective diffusion coefficients over the BAZ (e.g., D.D. Reible and Lampert 2014), although detailed modeling of the hydrodynamics and oxygen and contaminant transport has been conducted (e.g., Liu et al. 2019; Liu, Reible, and Hussain 2022). Simulating the BAZ and the mixing that occurs in the BAZ is critically important in a contaminant fate and transport model of the near-surface sediments. 

In surficial sediments, sorption of contaminants onto solids enhances the effects of bioturbation since organisms move both solids and the adjacent porewater. In deeper layers, however, contaminant transport by diffusion and advection (groundwater seepage) is retarded by sorption processes, which retain contaminant on the nonmoving solid phase (in a stable sediment environment). Models of the sediment environment need to be able to specify diffusion and advection as well as the partitioning into the solid phase that retards that movement. Partitioning in the sediment environment occurs between the water and the local solid phase (either sediments or a sorbing amendment such as activated carbon). Dissolved organic carbon (DOC) may influence partitioning, which can increase the amount of contaminant present in the porewater. Models require estimates of contaminant partitioning between the porewater and each of the phases that may retain the contaminant. Partitioning is often assumed to be governed by local equilibrium and constant phase–water partition coefficients, but nonlinear sorption may occur with strong sorbents such as activated carbon or at relatively high (near solubility) concentrations on natural sediments. It is known that amendments such as activated carbon adsorb contaminants at significantly different rates or time frames (e.g., kinetics) based on particle size (i.e., granular carbon adsorption is inherently slower than powdered carbon adsorption). Thus, the local equilibrium assumption may not be satisfied, and the kinetics of uptake should be considered explicitly. Sorption kinetic estimation is available in the CapSim model, and the model provides guidance for estimation of kinetic coefficients. If amendments are not uniformly distributed, this may also require explicit consideration during modeling, for example, through a sensitivity analysis. This is discussed further in Section 5.5.3. Models must be able to address both equilibrium partitioning and the kinetics of sorption to address these effects. 

The microbial community in the sediment environment also has a large effect on contaminants through changes in the sediment chemistry. Deposition of organic matter on the sediment surface drives an active microbial community that typically consumes oxygen within a few millimeters of the surface and successively reduces less favored electron acceptors including, in turn, nitrates, manganese, iron, and sulfates. In the near surface, more oxic conditions are conducive to hydrocarbon oxidation while the more reduced conditions at deeper depths encourage reductive dechlorination and the formation and precipitation of metal sulfides, reducing their availability. At the bottom of a surficial sediment layer, methane is produced if the sediment is sufficiently reduced and can be the source of gas formation and ebullition as it migrates to the surface. The entire range of processes from oxygen consumption at the sediment–water interface to methanogenesis at depth may occur within 10 cm of the surface, particularly in fine-grained, organic-rich sediment deposits. Even though these processes can be simulated in models, this is rarely attempted; instead, approximate boundaries of aerobic (the upper few cm) and anaerobic conditions (deeper depths) might be defined as layers within the sediment or cap simulation environment to allow different conditions or model parameters to be specified in those layers. Hydrocarbon degradation may occur much more rapidly in aerobic layers while methanogenesis and metals binding by sulfides may occur primarily in anerobic zones. By separating aerobic and anaerobic zones, these processes may be simulated. 

All models must manage the boundary conditions at both the bottom and top of the modeled domain. Typically, contaminated underlying sediment layers should be incorporated within the model domain to allow explicit modeling of processes, including contaminant depletion, within that layer. If the modeling domain extends below the depth of contamination, the bottom boundary can then be defined simply as a condition of zero concentration or flux. When the contamination is very deep or when groundwater is carrying contaminants into the modeling domain, a condition that ensures that the flux from outside of the domain is carried into the domain should be chosen. In this case, a conservative assumption may be to assume an infinite source of contamination into the model domain. 

The top boundary of the modeling domain is typically the surface water. Because of the speed of contaminant transport within the BAZ, this zone quickly adapts to the surface boundary condition. Specification of zero concentration at the sediment–water interface will tend to lower concentrations within the BAZ, perhaps unrealistically. A more appropriate boundary condition is one that ensures continuity of flux across the sediment or cap/surface water interface. Two such boundary conditions are (1) incorporating a mass-transfer coefficient with the overlying water (even if the water concentration is effectively zero) or (2) estimating the overlying water concentration of the contaminant being modeled as a representative average over time. Note that the flux is typically much less sensitive than concentration to the top boundary condition because it is often controlled by the flux through the CIL (D.D. Reible and Lampert 2014). The sensitivity of the top boundary concentration to the modeling assumption suggests that it is generally not appropriate to define a design criterion focused on concentration at the sediment–water interface. It is better to use a design concentration criterion lower in the cap (e.g., at the bottom or middle of the BAZ) or use a flux criterion directly. 

5.3 Summary of Available Modeling Tools for Cap Chemical Isolation Design 

5.3.1 RECOVERY Model 

RECOVERY is the USACE screening-level contaminant fate and transport model for assessing long-term impacts of contaminated bottom sediments on surface waters and ecological resources. The model was developed to estimate exposure scenarios during the risk assessment phase and to screen common sediment remedial alternatives. The model estimates contaminant interaction between the water column and the cap/bottom sediment, as well as between contaminated and clean cap/bottom sediments. RECOVERY is intended primarily for organic contaminants with the assumption that the overlying water column is well mixed vertically, but the model has been applied at numerous sites contaminated with heavy metals (copper, lead, selenium, nickel, and cadmium). The contaminant is assumed to follow linear, reversible, equilibrium sorption and (optionally) first-order decay kinetics. The system is physically represented as a well-mixed water column (i.e., zero dimensional) underlain by a vertically stratified sediment column (i.e., one-dimensional transport). The sediment is well mixed horizontally but segmented vertically into a well-mixed surface (active) layer and deep sediment. The specification of an active surface layer is included because an unconsolidated layer is often observed at the surface of sediments due to a number of processes including bioturbation and mechanical mixing (Boyer et al. 1994). The deep sediment is segmented into variably contaminated and clean sediment regions. 

Major improvements have been made to allow a user to better simulate advection through the bottom sediment such as groundwater flow and flow resulting from consolidation of the contaminated material, foundation, and/or cap. RECOVERY can be applied to rivers, lakes, embayments, harbors, estuaries, and ocean areas. 

The RECOVERY model calculation approach makes the following assumptions: 

• a well-mixed surface water column underlain by a vertically stratified cap/sediment column 
• variable contaminant concentration and cap/sediment properties 
• the movement of one contaminant is independent of the presence of other contaminants 

Calculations that drive RECOVERY use mass balance equations derived from within the water column and mixed sediment layer and a specific diffusion and bioturbation equation in the deep sediment layers. These differential mass balance equations factor in sorption, decay, volatilization, burial, resuspension, settling, bioturbation, and porewater diffusion. Components of the mass balance differential equations include partitioning of contaminant between the solids matter and water using a linear sorption mechanism; decay rate constants that reflect photolysis, hydrolysis, and bacterial degradation; volatilization; and a solids budget where the sediment mass is conserved using a steady-state mass balance for mixed sediment layer solids. 

The mass balance differential equations are solved numerically using an adaptive-step-size fourth order Runge-Kutta method for the water column and a forward difference Crank Nicholson solution for the bottom sediment. Initial conditions include multiple layers with variable concentrations and properties from the top of the mixed layer to the bottom of the contaminated layer. Boundary conditions of the model are set such that the mass flux of the contaminant is constant from the bottom contaminated sediment layer. Coupling between the contaminants in the mixed sediment layer and the deep sediment takes place by diffusive transfer as well as by the burial of contaminated particles from the mixed sediments layer into the deep layer. 

5.3.2 CapSim Model 

CapSim is an open-source one-dimensional model that simulates contaminant transport and reaction through sediment and caps for the purposes of assessing natural recovery processes and supporting cap and in situ treatment design. CapSim simulates fate and transport processes in both the porewater and solid phases based upon the interstitial or porewater concentrations of contaminants and can also be used to model conditions that affect contaminants, such as biogeochemistry of surficial sediments. Details of the CapSim model structure and underlying theory are described by Shen et al. (2018) and are summarized below: 

• Multiple media layers with varying input conditions 
• Multiple species with kinetic or equilibrium reactions and partitioning that can be used to model the contaminant and background conditions such as biogeochemical reactions 
• Media properties including sediments, conventional and amended cap materials, and sediment amendments, including commercially available materials 
• Diffusion/dispersion (in all layers with corrections for tortuosity and dispersivity) 
• Bioturbation via porewater or solids and adjusted for particle size 
• Hyporheic exchange 
• Groundwater upwelling and tidal or oscillating flows 
• Sediment consolidation, erosion, and deposition 
• Precipitation/dissolution modeling that can be used to simulate NAPL dissolution as well as solid-phase precipitation or dissolution 
• General boundary conditions at both the top and bottom of the modeling domain, including a control volume surface-water model, a mass-transfer boundary condition and a fixed concentration boundary condition at the top, and a flux-matching or specific concentration boundary at the bottom 

The governing numerical equations for the model use a mass conservation equation for a one-dimensional stratified system composed of multiple layers with various physical and chemical properties. The model simulates all layers as saturated porous media with the solid particles as immobile except near the surface where particles can move as a result of bioturbation, erosion, deposition, or consolidation. 

The mass loading of the contaminant in the mobile phase consists of the freely dissolved concentration and its DOC-associated concentration. The mass loading equations also factor in generation or consumption of the contaminant and other relevant species by reactions in porewater. Competition between sorption processes can be simulated by modeling reactions between sorbed and desorbed phases. A variety of sorption isotherms (linear, Langmuir, Freundlich) can be used to describe equilibrium or nonequilibrium relationships between the solid phase and porewater phase. Recent advances have incorporated tools to help estimate kinetics of activated carbon sorption as a function of particle size (e.g., GAC vs. PAC). In some cases, the use of GAC can also significantly reduce the number of carbon particles incorporated into a CIL (e.g., when very low carbon percentages less than 1% are required). Special care may be needed to assure uniformity of placement in such conditions and to ensure that the mean spacing between carbon particles is much less than the thickness of the capping layer (to avoid carbon bypassing). Models assume uniform mixing of amendments in amendment layers. Models can be used to evaluate nonuniformity of amendments through a sensitivity analysis. Metals transport and sorption can be simulated through simple partitioning relationships or explicitly modeled via surface complexation–type models. All factors that influence a contaminant (e.g., oxygen for aerobic degradation) should be included in simulations to fully evaluate contaminant dynamics. 

Vertical flux is calculated using diffusion, hydrodynamic dispersion, advection, and bioturbation equations. Hydrodynamic dispersion and advection are a function of groundwater flow/velocity, upwelling, porewater additions due to consolidation of sediment and capping, and tidal influence. Bioturbation from benthic organisms near the surface is factored into the mixing processes through effective diffusion models for both solids and porewater. The depth of bioturbation can be treated as a constant or as depth dependent. Additionally, deposition is simulated as a natural capping layer with increasing thickness over time. 

Initial conditions can be defined arbitrarily by setting a depth and concentrations within a layer. Solid and water phases can be assumed at equilibrium, or for kinetic evaluations they can start at different concentrations (e.g., contaminated sediment and porewater but initially clean activated carbon). Boundary conditions at the interface of two layers (porewater and solid phases) assume that the porewater concentrations and the fluxes are equal for mass continuity. Boundary conditions for the bottom boundary include fixed concentration or flux matching. The fixed concentration condition suggests an infinite contaminant source with a given concentration continually supplying contaminants to the cap, whereas the flux-matching condition models a constant upwelling advective flux from the sediments below. If there is no upwelling, the flux- matching condition assumes zero contaminant flux from below. The flux-matching condition is in general more accurate but typically less conservative than a constant-concentration condition. 

The numerical solution to the CapSim model includes finite-difference methods using an implicit method. All nonlinear terms are solved at each time step by Newton’s method. The deposition of sediment is modeled by a special layer with a growing number of grids to imitate the accumulation of solid materials and is averaged over the time span associated with growth. 

Examples are provided with the model to illustrate its usage and include an example that solves for the detailed biogeochemistry of the surficial sediments or cap layer. The model is structured such that the more complicated situations (chemical reactions, kinetics of sorption, etc.) need not be specified if no data exist, but these features can be added in as data become available or to conduct sensitivity analyses. Pop-up boxes are used to estimate parameters (e.g., bottom mass-transfer coefficients and activated carbon sorption kinetics), if desired. CapSim can also be run in batch mode without the graphical user interface for multiple simulations, such as in sensitivity or Monte Carlo analysis. 

Similar to RECOVERY, CapSim can be applied to rivers lakes, embayments, harbors, estuaries, and ocean areas. 

5.4 Defining Modeling Objectives 

The model set up to predict the performance of a cap is informed by the design criteria described in Section 3. For many sites, it is necessary to make decisions that are informed by the design criteria when modeling the remedy performance. Some considerations are listed below: 

• Selecting overall performance objectives for modeling: This includes specification of a concentration or flux at a particular location as well as how this criterion is reflected in an areawide remedial effort. Capping is an areal remedy and is well suited for achieving goals such as reducing a sitewide SWAC, which can be evaluated on a bulk sediment or porewater concentration basis. In some cases, capping is also used to meet criteria on a point-by-point basis (e.g., to reduce risk to benthic organisms). 
• Selecting COCs for the basis of modeling: Some sites have many organic and inorganic COCs with remediation and/or background concentration goals. To simplify the modeling, the number of COCs evaluated can be limited to those that will most likely drive the design. 
• Selecting design evaluation depth for modeling: The design evaluation depth or compliance depth is the depth within the cap at which performance targets are assessed. Performance targets are discussed in Section 3.1. Design evaluation depths are discussed in Section 3.2.1. 

5.5 Model Inputs 

The components of the cap included in the model domain and the typical model inputs to a cap model are described below. For a complete guide to model inputs, please refer to the model-specific documentation. For CapSim, refer to Shen et al. (2018) and (Danny Reible, Shen, and Lampert 2021). For RECOVERY, refer to (Carlos E. Ruiz, Aziz, and Schroeder 2001) and (Boyer et al. 1994). 

5.5.1 Model Domain 

As described in Section 2, key cap functions may be performed by either a single or multiple layers. Although this section focuses on the CIL design, the model may include some or all of the layers discussed in Section 2 (either as part of the basecase design or sensitivity analysis) because these layers may provide some contaminant attenuation and therefore affect the long-term performance of the cap. In addition to the placed cap layers discussed in Section 2.4, the model may consider long-term sediment deposition over the cap surface as well as the sediment beneath the cap. These potential components of the model domain are discussed below, in order from top to bottom. 

5.5.1.1 Sediment Deposition 

Deposition in the model adds to the thickness of the model domain over time and increases the distance between the CIL and the BAZ, which provides additional attenuation distance. The addition of organic matter into the cap as a result of deposition will increase organic COC mass retention in the cap surface layer. If deposition of new sediment layers is modeled, it is important to evaluate location-specific sediment deposition rates and COC concentrations in the depositing material for use in the model. For example, areas more prone to scour, such as between bridge abutments and pier constrictions (where complex hydrodynamics cause flow acceleration and convergence), may experience different deposition rates than other areas of a site. 

When considering deposition in the modeling evaluation, it is important to account for long-term net deposition rates, rather than gross deposition rates. It may also be important to include deposition in the model if it contributes contaminants to the surficial sediments that could result in elevated concentrations relative to the performance targets at the compliance depth. If the surficial cap layers are sand or gravel, the BAZ may not form until deposition of organic-rich material occurs. This aspect of the cap performance may be accounted for in the design modeling or only in the sensitivity analysis to demonstrate the conservatism of the design approach in this regard. 

5.5.1.2 Erosion Protection and Habitat Layer 

The erosion protection layer does not typically provide much sorption because it is often composed of inert coarse-grained materials with low total organic carbon (TOC) (e.g., sand, gravel, rock) but may provide a thicker layer (increasing attenuation distance) to reduce transport of COCs to the long-term BAZ. As described in Section 3.3.1, in an advection-dominated system, increased thickness may not have much impact. The erosion protection layer may limit the formation of a BAZ in the lower cap layers. The habitat layer also provides attenuation distance, and depending on the material selected, may provide additional sorption capacity beyond the CIL. The decision about whether to include these layers in the model domain depends on the following considerations: 

• Erosion Protection: Sands and gravels that function as erosion protection are often included in the model domain because these layers provide attenuation distance. If the armor stone is large enough (e.g., rip rap), the void space may be so large that the material does not provide attenuation. In these cases, the erosion protection layer could be excluded from the model domain; however, the pore volume between armor stones may be subject to infilling by deposited sediment that fills these voids over time. This is different from the deposition layer described above, which adds thickness on top of the cap, rather than filling in the pore spaces as described in this paragraph. The depositing sediment may have an assumed initial COC concentration equal to current suspended solids in equilibrium with current surface water concentrations or a fraction thereof, assuming remediation and source control will reduce those concentrations over time. All areas of the cap will be subject to this deposition process, although periodic forces (e.g., high surface water flow velocities) may scour deposited sediment accrued over the cap in some areas. Even if no net accumulation occurs, natural organic material will still be added to the cap via bioturbation and infilling of pore spaces where the surface layer consists of armor stone. 
• Filter Layer: A filter layer may be needed to prevent piping of CIL material through overlying armor. This function may be accomplished by a geotextile or placement of a layer of material that is smaller than the armor stone and larger than the CIL material. If this layer is needed in the cap design and a granular material is used (rather than a geotextile), it is often included in the model domain because it provides attenuation distance. 
• Habitat Layer: A habitat layer may be placed on top of the cap for the purpose of providing suitable habitat for aquatic organisms. Depending on the nature of the erosion protection layer or CIL, either may also function as a habitat layer. In cases where a habitat layer is placed over an erosion protection layer, it may not be expected to remain in place (or mixing within that layer may be expected). In this case, it is suggested that all or part of the habitat layer be excluded from the model domain. 

5.5.1.3 Underlying Sediment 

The thickness of underlying sediment that must be modeled can be significantly less than the contaminated layer if key results (e.g., concentration at the bottom of the underlying sediment layer or concentrations at design evaluation depth) are not sensitive to the thickness of the sediment layer. The underlying sediment layer is typically modeled to assist in managing the boundary condition at the bottom of a CIL; a layer as thin as 15 to 30 cm is often sufficient. The underlying sediment layer may be conservatively modeled and assumed to have no depletion of concentrations over time (i.e., an infinite source of COCs to porewater) by simply specifying a constant concentration at the bottom boundary. 

5.5.2 Summary of Model Inputs 

Table 5-1 lists key model input parameters. Inputs for which the model is most sensitive are further discussed in Section 5.6. 

Table 5-1. Key model input parameters 

Parameter	Explanation for CIL Modeling Assumption
COC-Specific Input
COC Concentrations	Capping is an areal remedy; therefore, using a 95% UCL of the mean is suggested and considered to be appropriately conservative. Use of an average, percentile, or a maximum may be considered based on availability of data, CSM, site-specific factors, and preference for conservatism. Understanding the distribution of COC concentrations is an important factor to consider when evaluating whether the site should be subdivided to better account for the variability in the cap design. Use post-dredge concentrations if dredging will be conducted to accommodate the cap. A more detailed discussion is included in Section 5.5.3.1.
DOC Concentration	DOC in cap material–porewater may be assumed, conservatively, equal to the sediment-porewater DOC. Note that partitioning to DOC should not be simulated separately if already implicitly included in the site-specific measurements. If freely dissolved concentrations are available (e.g., through partitioning passive sampling), the partitioning to DOC should be included separately. Alternatively, values can be selected based on a literature review.
COC Degradation	The modeling can be simplified to exclude aerobic and anaerobic biodegradation of organic COCs, which is conservative for some chemicals.
Reactions	When using a model like CapSim or RECOVERY, reactions are typically assumed to be first order. Complicated reaction networks (e.g., reactants and products that are linked and nonlinear) can also be simulated in RECOVERY and CapSim (Danny Reible, Shen, and Lampert 2021).
Cap Material Input
Cap Material–Porewater Partition Coefficients	Measured average values accounting for a range of site-specific COC concentrations (see Case Study No. 3 in Appendix A), competitive sorption of chemicals, and DOC effects are preferred. Note that partitioning to DOC should not be simulated separately if already implicitly included in the site-specific measurements. If freely dissolved concentrations are available (e.g., through partitioning passive sampling), the partitioning to DOC should be included separately. Alternatively, values can be selected based on a literature review.
DOC Partition Coefficient	DOC partition coefficients may be informed by a literature review. If the site-specific partition coefficients are determined and account for the effect of DOC on partition coefficients by measuring freely dissolved contaminant concentrations in porewater, in addition to the COC concentrations associated with DOC, DOC partition coefficients may be assumed as zero for modeling purposes.
Amendment Dose	Amendment dose is a design variable that is often defined through an iterative approach to meet the design criteria. The specifications may include provisions to verify that the average required dose is met. Overdose is not included in the model during the design phase. If conducting post-construction audit modeling, the placed amendment dose should be used in the modeling. Post-construction audit modeling is discussed in Section 5.7.
Transport Properties
Seepage Rate	Average site-specific calculated Darcy velocity based on empirical measurements is preferred. The model CapSim can simulate oscillating Darcy velocity, such as in situations where the site is influenced by tidal fluctuations. Section 5.5.3.4 provides more details.
Deposition	Modeler may choose to include deposition in the basecase modeling or evaluate it as part of sensitivity analysis to demonstrate conservatism of the CIL design modeling. Deposition may also be included to account for recontamination and its effects on meeting design criteria.
Mass-Transfer Coefficient	The benthic boundary layer (i.e., the sediment–water interface) mass-transfer coefficient for each COC at the cap-water interface can be estimated based on the Thibodeaux (1996) equation or the Chilton-Colburn analogy developed by Chilton and Colburn (1934) and also described by Welty, Rorrer, and Foster (2014) .
Hydrodynamic Dispersivity	The CapSim Quick Start Manual (Danny Reible, Shen, and Lampert 2021) recommends using a dispersivity coefficient equal to 5% to 10% of the layer thickness and using a minimum value of 1 cm. Empirical relationships for groundwater dispersion may also be applicable.
Tortuosity Correction	A variety of models are available for this correction, and CapSim provides separate estimates typically applied to granular material such as sand and consolidated sediments.
Depth of Bioturbation	The USEPA (2015b) recommends a typical BAZ depth of 10 to 15 cm in most estuarine and tidal freshwater environments, 15 cm in lentic (still water) environments, and from 15 cm to 35 cm in lotic (fast-moving water) systems, depending on water depth and habitat type. Bioturbation may be limited in the sand/armor layer immediately after construction of the cap due to low TOC. TOC typically increases over time as fine-grained sediment deposits on top of and mixes into the cap surface or forms on top of the cap. Higher TOC can support a greater abundance of benthic organisms. Although the depth of bioturbation may be minimal immediately after cap construction, for the purposes of modeling it is general practice to assume the full depth of bioturbation that is anticipated in the future.
Biodiffusion	Range of values are provided in Danny Reible, Shen, and Lampert (2021).
Sediment Input (If Explicitly Simulated)
Sediment-Porewater Partition Coefficients	Same as cap material–porewater partition coefficients, except that in situ measurement is also an option (see Case Study No. 3 in Appendix A).
Thickness/Layers	As defined by variations in measured sediment properties or concentrations, but often deeper sediment zones may have minimal impact on near-surface behavior.
Porosity and Dry Density	Average site-specific measurements are preferred. These parameters may not be measured by the lab. If not, porosity and bulk density can be estimated using percent moisture or percent solids (a typical measurement by the laboratory) and an assumed specific gravity of the solid particle (e.g., 2.6 g/cm3).
Consolidation	Sediments can consolidate under the weight of a cap, resulting in porewater being expressed (i.e., an addition to the seepage rate). In cases where dredging occurs before cap placement, consolidation may be minimal, if any occurs. Depth of consolidation and time to reach 95% consolidation are parameters that can be calculated from geotechnical evaluations and are used in CapSim to estimate consolidation-related porewater expression and associated contaminant transport.

Acronyms and Abbreviations: 
BAZ = biologically active zone 
CIL = chemical isolation layer 
COC = contaminant of concern 
cm = centimeter 
CSM = conceptual site model 
DOC = dissolved organic carbon 
g/cm³ = gram per cubic centimeter 
TOC = total organic carbon 
UCL = upper confidence limit 
USEPA = United States Environmental Protection Agency  

5.5.3 Key Model Inputs 

The following parameters typically have significant impacts on the cap design: 

• COC concentrations: In general, areas with higher COC concentrations in porewater require a more robust CIL. 
• Sediment deposition rate: If deposition is expected to occur and depositing sediments are clean (e.g., have COC concentrations less than RGs), simulating even small rates of deposition can show a large benefit to long-term chemical isolation performance.  
• Cap material partition coefficients: CIL materials typically evaluated include sand, natural organic matter (NOM), organophilic clay, GAC, and PAC. Several other materials are available and are discussed in Section 2.3. 
• Seepage rates: Higher seepage rates result in faster COC transport via advection and require a more robust CIL. 

The following subsections discuss these key inputs in more detail. 

5.5.3.1 Contaminant of Concern Concentrations 

COC concentrations define the boundary condition, initial concentrations in the sediment, cap layers, and depositing particles. Depending on the model used, the input to the model is on a porewater basis. Based on contaminant distribution, porewater data should be collected at a statistically adequate spatial density over the footprint of the capping area(s) for all site-specific COCs. In the absence of measured porewater concentrations, dry-weight sediment COC concentrations obtained from sampling may be used to estimate porewater concentrations in each sample using the sample-specific fraction of organic carbon (for organics) and the partition coefficient¹. Equation  5-1 is used to estimate sample-specific porewater concentrations. 

Equation 5-1: 

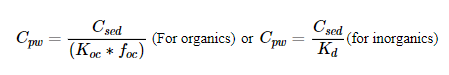
Where: 
C_pw = Calculated porewater concentration (micrograms per liter [µg/L]) 
C_sed = Measured sediment concentration (micrograms per kilogram [µg/kg]) 
f_oc = Measured fraction of organic carbon associated with each sediment sample (unitless) 
K_OC = Site-specific organic carbon–porewater partition coefficient for organics (liters per kilogram of organic carbon) 
K_d = Site-specific distribution coefficient for inorganics (liters per kilogram) 

When dealing with nondetect concentrations, it is common to assume the quantitation limit for individual COCs and zero or half of the quantitation limit for chemicals that are summed to calculate a total concentration (e.g., total PAHs, total PCBs, dioxin/furan toxic equivalency. Cap material solid-phase concentrations are often defined by measurements from the borrow source or assumed to be zero. Initial porewater concentrations in a cap are typically assumed to be equal to the surface water concentration. Note that when initially placed, the porewater concentration within the cap material may be equal to the concentration in surface water because the surface water is entrained in the pore space as the material is being placed through the water column. 

5.5.3.2 Sediment-Porewater Partition Coefficients 

Partitioning describes the relationship of chemicals between the dissolved and sorbed phases (i.e., between porewater and sediment or cap material). The COC concentrations in the porewater at equilibrium (C_pw) and in the sediment at equilibrium (C_sed) can be measured to determine sediment-porewater partition coefficients. Partition coefficients are calculated for each sample for each organic or inorganic COC as shown in Equation 5-2 below. 

Equation 5-2: 

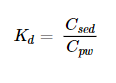
Where: 
K_d = adsorption-desorption distribution coefficient 
C_sed = COC concentration in the sediment at equilibrium (COC mass/sediment mass) 
C_pw = COC concentration in the porewater at equilibrium (COC mass/water volume) 

For multiple samples, the K_d is the average of the ratio of concentrations in sediment to porewater. 

For organic partition coefficient calculations, sediment concentrations are typically normalized to TOC. In the absence of site-specific partition coefficients, literature values may be used. 

5.5.3.3 Cap Material Partition Coefficients 

Unamended Cap Material 

The partition coefficient of unamended capping materials needs to be understood and incorporated into modeling. Partition coefficients for the cap material can be the same as the partition coefficients used to represent the sediment (see Section 5.5.3.1), but that is not always the case. In some cases, a value from the literature may be the best way to represent cap material. For example, if site-specific partition coefficients based on porewater and sediment are different from literature values and those differences can be explained by site-specific conditions that would not be present in the cap, then literature values may be used to reflect cap material. 

If the site-specific partition coefficients are different from values in the literature, it is good to understand what may be causing that difference and consider whether the cause for the difference is likely to occur in the cap. For example, the presence of black (or soot) carbon in sediments often causes the organic carbon partition coefficients for organic compounds to be higher than reported in the literature. Black carbon will not be present in the cap; therefore, use of the site-specific partition coefficient developed from site sediment and porewater is not appliable to the cap. A separate study to develop partition coefficients applicable to the cap material or the use of literature values are preferred in this case. 

Amended Cap Materials 

Isotherm testing may be completed to evaluate the sorption of COCs onto the amendments. If site-specific testing is not conducted, literature values may be used, although isotherms derived from the literature may not account for particle size differences (e.g., GAC vs. PAC), competition of sorption sites for the full suite of chemicals present in the sediment porewater at a site, the potential for fouling or dechlorination and the formation and precipitation of metal sulfides, or the competitive effects of NOM. It may be appropriate to reduce the sorptive capacity of activated carbon by a factor of 2 to 5 to account for the effects of NOM. In addition, it is critical that any isotherm testing use the actual commercially available materials contemplated for the cap design and are tested for the anticipated residence time that the COCs will reside within the cap. Sorbents without a nanometer-scale pore structure (such as organophilic clay) show little effects of NOM. For site-specific batch treatability testing, COCs are added to slurries of amendments and water. The water may be sourced from site surface water, porewater from centrifuged sediments, or synthesized (e.g., by adding seawater salts to freshwater). NOM can be added to achieve site-relevant DOC concentrations. Due to the sorption capacity of some amendments, passive sampling may be needed to achieve the detection limits necessary to quantify partitioning. 

The effect of co-sorption on sorptive capacity, which can occur due to DOC and other chemicals competing with COCs for sorption sites, are directly accounted for in partition coefficients that are derived from actual site porewater (containing site DOC and site COCs). 

Equilibrium (i.e., post-test) porewater concentrations for the organic COCs are determined using post-test passive sampling data and measured directly by analysis of post-test aqueous samples for inorganic COCs. 

To determine the equilibrium COC concentrations in the sorbent, a mass balance approach is used.² Pre- and post-test COC mass in the water, post-test COC mass in the passive sampler, background COC mass in the passive sampler, and the cap material are used to estimate COC mass sorbed by the cap material. It is critical to understand that both treatability testing and modeling are assuming a theoretical ideal or perfect distribution of amendment materials (sorption) of COCs within the CIL, which is not generally obtainable during construction of the cap. Modeling of nonuniform distribution can be performed to evaluate actual results of placement of amendments and impact on performance. 

Once the porewater and sorbent equilibrium concentrations are obtained, the data may be used to evaluate partitioning relationships. As examples, Freundlich isotherm and linear isotherms are discussed below. The choice of isotherm selected is based on the fit to data. 

Freundlich Isotherm 

Equation 5-3: 

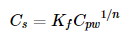
Equation 5-4: 

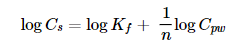
Where: 
C_s = COC concentration in the sorbent at equilibrium (µg/kg)  
K_f = Freundlich’s constant (the intercept of the fitted line to the log C_s versus log C_pw plot represents log K_f, [µg/kg]/[µg/L]^1/n) 
C_pw = COC concentration in the porewater at equilibrium (µg/L) 
1/n = Exponent of nonlinearity (the slope of the fitted line to the log C_s versus log C_pw plot, unitless) 

Linear Partitioning 

Equation 5-5: 

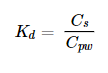
Where: 
K_d = COC partition coefficient between sorbent and porewater (the intercept of the fitted line to the log C_s versus log C_pw plot with slope forced to one, water volume/cap material mass) 
C_s = COC concentration in the sorbent at equilibrium (COC mass/cap material mass) 
C_pw = COC concentration in the porewater at equilibrium (COC mass/water volume) 

Direct use of the measured data essentially assumes that the absolute uncertainty in each concentration measurement is the same. Sometimes log-transformed C_s versus log-transformed C_pw data are used, which effectively assumes that the relative error in all samples is the same. 

5.5.3.4 Groundwater Seepage Rates 

Groundwater seepage rates can be estimated through a variety of sampling methods. Types of seepage meters include drum and bag and ultraseep meters. The selection of the sampling locations may be informed by distributed temperature sensing mapping results. Vertical hydraulic gradients can be measured using colocated differential pressure piezometers and hydraulic conductivity. The vertical hydraulic gradient and Darcy velocity (or seepage rate) measurements are related by the following Darcy’s law equation: 

Equation 5-6: 

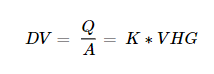
Where: 
DV = Darcy velocity (centimeter per year) 
Q/A = Direct seepage measurement (centimeter per year) 
K = Vertical hydraulic conductivity (calculated, meters per year) 
VHG = Direct vertical hydraulic gradient from piezometers (centimeter per meter) 

The New Jersey Department of Environmental Protection (2016) and references therein recommend using a multiscale approach to determine groundwater to surface water interactions and combining multiple techniques because of the limitations and uncertainties associated with the various methods. Additional methods to estimate Darcy velocity include the following: 

• modeling the Darcy velocity by fitting a model to a measured profile of a nonreactive chemical (e.g., chloride, salinity, etc.) 
• estimating based on a water budget evaluation informed by estimates of the groundwater recharge rate from the larger watershed to the watershed draining to the cap area 
• estimating based on groundwater flux from calibrated upland groundwater models 

5.5.3.5 Specific Consideration for NAPL 

NAPL can influence contaminant partitioning and influence contaminant migration or retention directly through mechanisms such as the following: 

• gas ebullition, which may transport NAPL from the sediment to the water surface, producing sheens 
• NAPL advective migration as a continuous fluid phase within the sediment pore spaces 
• Post-capping sediment consolidation (i.e., squeezing) and concomitant pore space reduction due to the weight of the cap, resulting in upward movement of porewater and, possibly, NAPL 

Cap models are not designed to directly address NAPL mobility. In some cases, this may be addressed by superimposing a contaminant flux associated with gas ebullition or NAPL migration. CapSim allows for the calculation of partitioning to and from an immobile NAPL phase and dissolution of the NAPL through incorporation of precipitation/dissolution reactions within the modeling framework. 

5.5.3.6 Approach for Selecting Model Input Values 

The best models are those that most accurately reflect real-world conditions. Environmental data are often variable, both spatially and temporally, which adds uncertainty. Uncertainty can be addressed by adding reasonable and appropriate conservatism into the modeling approach. As discussed in Section 3.2.3, reasonable and appropriate conservatism is achieved by balancing the level of conservatism assumed for individual parameters, to reduce uncertainty, but avoiding excessively compounding conservatisms, which results in a scenario that is not representative of likely future conditions. For example, groundwater seepage and porewater concentrations in sediments underlying the cap are two key parameters. Within a cap footprint, chemicals in porewater have a range of concentrations and vary spatially and with depth. In addition, groundwater seepage rates may vary spatially and temporally. Pairing the maximum porewater concentration with the maximum instantaneous groundwater seepage rate is conservative, but may be too conservative, resulting in a cap design that is unnecessarily costly and potentially more challenging to construct. When surficial sediments are the primary concern (as opposed to contaminated groundwater, for example), it is often the case that lower porewater concentrations are observed where seepage rates are the highest because the chemical has been flushed. Thus, it is important to understand the CSM when selecting model input values and select appropriately conservative values that align with the goals of the project. Section 5.6 provides options for addressing uncertainty and conservativism in design. 

5.5.3.7 Interpreting Model Predictions 

The model results should be interpreted within the context of the model objectives (see Section 5.4). Some considerations include the following: 

• The concentration or flux through the cap should be predicted conservatively. Although capping is an areal remedy, designs might focus on individual portions of the site or be optimized for different areas of the site, depending on the heterogeneity of the site conditions. Statistics describing physical characteristics can be used to define subareas for particular designs components, including the delineation of zones requiring a more robust design. Within a subarea, a design is often defined on a conservative basis. Selecting the 95% UCL on the mean porewater concentration of a COC within a subarea as a model input parameter is considered an appropriately conservative approach. In cases where there are insufficient data to calculate a 95% UCL for COC concentrations, maximum concentrations can be used as a conservative approach. For seepage rates, simulating a rate that is most representative of long-term values is most appropriate. For example, in a tidally influenced area, seepage rates may vary over the tidal cycle; at low tide the seepage rate is highest, and at high tide the seepage rate is the lowest. It is unrealistic to assume a seepage rate that is equivalent to the low-tide value throughout a long-term model simulation. Under this scenario, the best approach is to simulate the variable rate. Another option is to select a long-term average, which accounts for the highs and lows, and simulate the mixing that occurs due to the reversals in flows by modifying dispersion. 
• The evaluation of a cap should be focused on the COCs that are most likely to drive the design. For example, a CIL may be designed for the chemical(s) with the highest concentrations in sediment compared to the design criteria (i.e., require the greatest reduction in concentration to meet the design goal) and those with the highest mobility. A CIL design that is protective of the most-mobile COCs will be protective of chemicals that are less mobile and require a lower reduction in concentrations (or are already below the design criteria). In addition, some sites have design criteria for groups of COCs, such as total PAHs, total PCBs, or dioxin/furan toxic equivalency concentrations. If RGs include groups of COCs, the modeler may simulate total concentrations and use select input parameters, including partition coefficients, that are representative of those groups instead of modeling an individual representative COC from those groups. But combining individual compounds with significantly different physical properties will limit the ability of the model to accurately predict contaminant transport. For example, using an average partition coefficient to represent a group of chemicals will underpredict the mobility of some of the chemicals in that group and overpredict the mobility of others. A more representative, but more time-consuming, choice is to model individual chemicals or combine similar compounds, such as PCBs with equal numbers of chlorine atoms (homologs) or PAH compounds of the same number of rings and sum the results of these individual chemicals or homolog groups to compare to a total criterion. Models such as CapSim can simulate the behavior of multiple contaminants simultaneously. 
• As described in Section 3.2.1, the point of compliance describes the depths(s) over which the RAOs apply. The design evaluation depth is the depth within the cap where model-predicted concentrations are compared to the target concentrations. In many cases, the design evaluation depth may be the same as the point of compliance. 
  • If the cap performance targets are based on the protection of benthic organisms, the appropriate point of compliance is within or at the bottom of the BAZ. 
  • If the cap performance targets are based on the protection of fish (or higher trophic level organisms), which are present in the overlying surface water, then flux to the water column may be more appropriate, though understanding the pathway of chemical concentrations to the fish is important (i.e., benthic feeding fish vs. water-column feeders). As noted in Section 5.2, concentration and flux are influenced by the choice of top boundary condition. 

A modeler may choose a design evaluation depth that is more conservative than the compliance depth (i.e., depth required to meet performance targets). For example, if the concentrations within the BAZ must meet the performance targets, then designing the cap to meet the performance targets at a depth that is deeper than the BAZ is more conservative. If a more conservative design evaluation depth is selected for modeling purposes than the point of compliance, it is important to account for this conservative choice in the selection of input parameters to balance the level of conservatism in the design.  

5.6 Sensitivity and Uncertainty 

Sensitivity and uncertainty analyses are critical considerations of modeling. Sensitivity refers to the extent to which model results change when the value of a parameter changes. Uncertainty is the more general concept and refers to the overall reliability of the model or model input value as a reflection of actual conditions. A number of guidance documents and technical literature related to sensitivity and uncertainty analyses in modeling exist (e.g., USEPA 2009). This guidance summarizes some of those key concepts and includes additional suggestions related to cap modeling specifically. 

Two types of uncertainty relevant to cap modeling include model framework uncertainty and model input uncertainty. Uncertainty in the model framework is a function of the model’s ability to simulate the processes that are part of the CSM. Sometimes simplistic models have been used for specific purposes in cap design. In addition, models such as CapSim or RECOVERY are subject to continuous improvement and better characterization of sediment processes (e.g., Shen et al. 2018). Using more recent versions of available cap models minimizes the uncertainty associated with model framework. 

The remainder of this section describes model input uncertainty. As described in the previous section, the modeling to design a CIL should use model inputs that incorporate reasonable and appropriate conservatism, with the goal of creating a simulation that is representative of actual conditions. Understanding which model inputs are most sensitive (i.e., have the greatest impact on model results) and which are most uncertain is key to defining the most appropriate model input values for designing a protective CIL. Together, sensitivity and uncertainty analyses provide an understanding of the confidence that may be placed in model results. Figure 5-4 illustrates the relationship between model parameter sensitivity and uncertainty and how they work together to influence the model results. Model inputs that are more uncertain but not sensitive will not have a large impact on the model results. Similarly, model inputs that are more certain and sensitive also do not have a large impact on model results and, therefore, have a smaller impact on the design. Model inputs that are more uncertain and for which the model is most sensitive (upper right corner of the graphic) have the greatest impact on the model results and, therefore, a greater impact on the design of the CIL. The basecase cap configuration should be evaluated under an alternative scenario in this case. 

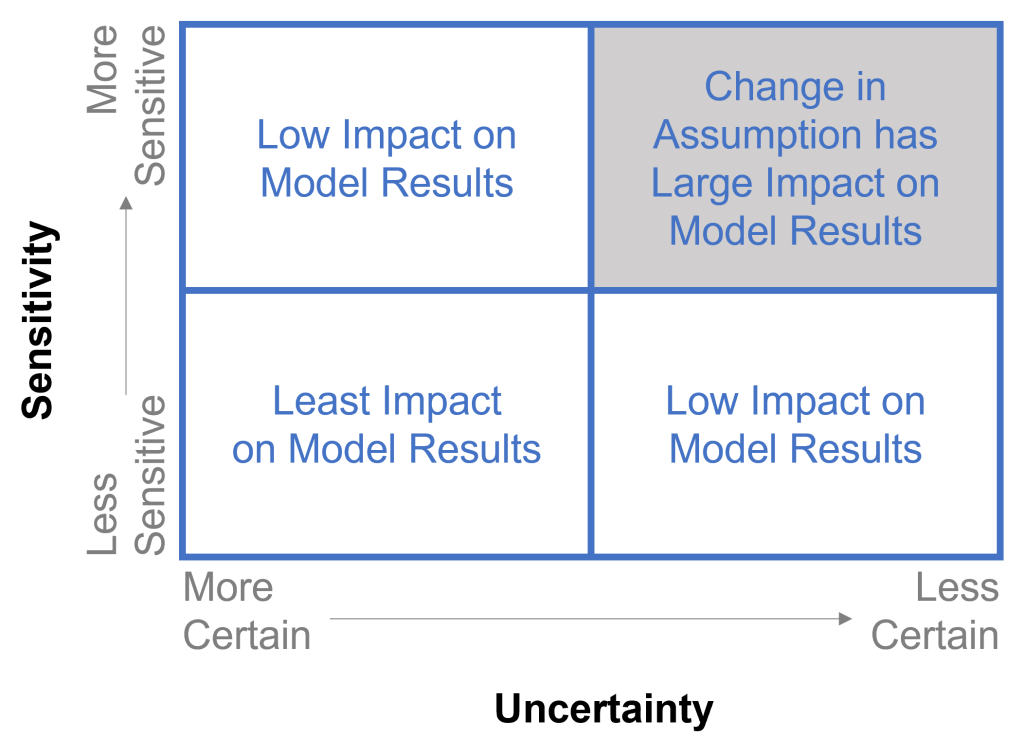
Figure 5-4. Impact of uncertainty and sensitivity on model results. 

Source: D. Reidy. Used with permission.

The parameters that most influence model results can be found through simulations using a range of values for model parameters. In general, capping models are most sensitive to seepage rates and chemical concentrations in the sediment porewater beneath the cap. To evaluate model sensitivity to other input parameters, start by modifying the model input parameter values one at a time and assessing how the model results change. From this type of analysis, the magnitude of the change in model input value and the change in the model result can be evaluated. CapSim contains capabilities to run Monte Carlo simulations around specific parameters to output ensemble average model results. 

An uncertainty analysis is similar to a sensitivity analysis and is often referred to as such in practice. But the purpose of an uncertainty analysis is to understand how changes in uncertain model input values affect the results of the model and, therefore, the design of the CIL. 

When evaluating uncertain model inputs, it is tempting to design the CIL (i.e., thickness and amendment type and content) necessary to meet the design targets for a basecase and upper-bound or lower-bound input parameter values. This approach results in multiple cap designs—one for each set of model input parameters. But the development of multiple designs raises the question of which design should be constructed. Instead, design a cap (thickness and composition) that meets the performance targets under the basecase scenario. Then, the input values for the uncertain parameters are varied (within the range of uncertainty) for the thickness and composition determined under basecase conditions. The model results are then compared to those of the basecase scenario to determine how the protectiveness of the CIL changes with the change in the model input value. As an example, if the cap configuration for the basecase scenario meets the target performance criteria for 100 years, it is helpful to know how long that same cap configuration meets the target performance criteria using the alternative (higher or lower) model input value. The results can then be used to determine whether that level of uncertainty is acceptable. Things to consider when deciding whether that level of uncertainty is acceptable include the following: 

• Acknowledgment that overplacement and overdosing may be included in the construction specifications. Placement and dosing tolerances are discussed further in Section 6. 
• The likelihood of the alternative value should conditions change. 

The results of the model sensitivity analysis may result in one of the following actions, depending on the level of uncertainty that is acceptable: 

• Collecting more data to increase certainty in the model input value and refining the modeling with the updated value. 
• Adding a factor of safety to the cap configuration (i.e., thickness or composition). 
• Designing the cap for the upper-bound value for the uncertain parameter if the value is highly uncertain and the results of the sensitivity analysis indicate a cap may not be protective for an acceptable period of time. 

5.7 Post-Construction Audit 

Unlike other models, such as hydrodynamic, groundwater, surface water quality, and chemical fate and transport within sediments, model calibration is uncommon (if ever used) in cap modeling. QA/QC during construction is critically important because it verifies that design specifications are met. Performance monitoring provides an opportunity for verifying long-term cap chemical isolation. Models simulate idealized situations, and a post-construction audit is useful for understanding how well the idealized model predicted future conditions. Post-construction audits are useful for learning from previous experiences. These types of evaluations should be conducted following cap pilot studies to better understand the site and inform the subsequent full-scale design. Post-construction audit modeling is also useful for informing future cap designs in the same or similar settings, informing cap maintenance plans, validating long-term cap monitoring results, and informing the scope and frequency of long-term cap performance monitoring. For example, the post-construction audit can be a valuable line of evidence for interpreting confounding factors influencing long-term monitoring results, like deposition of contaminated sediments over the surface of a cap. 

5.8 Model Documentation 

Documenting the model approach, input parameter values, and results is important for stakeholders to understand the basis for the cap design. Documentation should be done in such a way that others can easily follow what was done and repeat it, if necessary. The following list outlines the components that should be included in model documentation: 

• The model (and version of the model) used to conduct the modeling, with citations, should be documented. 
• Model inputs and assumptions: 
  • The names of the model input parameters in the model. 
  • The values used in the model (basecase and range, if sensitivity analysis is conducted), including the units of the value. 
  • The source and rationale for the value used in the model. This includes a summary of the data used to develop model input values. Include citations, where necessary. 
• Presentation of model results could take many forms, including the following: 
  • A table of model results, including values for comparison to the design criteria. 
  • Figures that show temporal trends in concentrations over the course of the design life. This type of documentation is helpful for stakeholders to understand the trajectory of concentrations or fluxes and how those concentrations or fluxes may change immediately after the design life. 
  • Figures showing depth profiles. These could be helpful ways to show the vertical migration of the chemical over time. 
  • Communication about the uncertainties in the model results and suggestions for future phases of design (if not the final design).

¹ CapSim 4.0 does allow the modeler to input a sorbed-phase concentration, and the model calculates the porewater concentration. 

² The biodegradation process is not included because a biocide is added to the test jars to inhibit biodegradation.